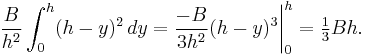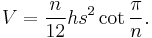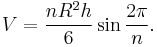Pyramid (geometry)

Set of pyramids
Square Pyramid
Faces n triangles,
1 n-gon
Edges 2n
Vertices n + 1
Symmetry group Cnv
Dual polyhedron Self-dual
Properties convex
The 1-skeleton of pyramid is a wheel graph
This article is about the polyhedron pyramid (a 3-dimensional shape); for other versions including architectural pyramids, see Pyramid (disambiguation).

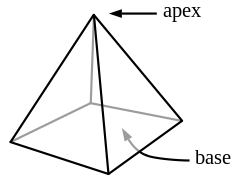
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base.

A pyramid with an n-sided base will have n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.

When unspecified, the base is usually assumed to be square.

If the base is a regular polygon and the apex is above the center of the polygon, an n-gonal pyramid will have Cnv symmetry.

Pyramids are a subclass of the prismatoids.

Contents

Pyramids with regular polygon faces

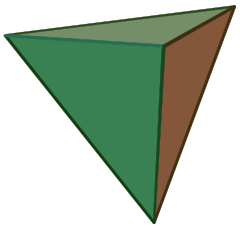
The regular tetrahedron, one of the Platonic solids, is a triangular pyramid all of whose faces are equilateral triangles. Besides the triangular pyramid, only the square and pentagonal pyramids can be composed of regular convex polygons, in which case they are Johnson solids.

Tetrahedron Square pyramid Pentagonal pyramid
Tetrahedron.svg Square pyramid.png Pentagonal pyramid.png

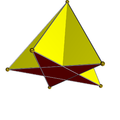
Star pyramids

Pyramids with regular star polygon bases are called star pyramids. For example, the pentagrammic pyramid has a pentagram base and 5 intersecting triangle sides.

Pentagram pyramid.png

Volume

The volume of a pyramid is 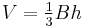V= \tfrac{1}{3}Bh where B is the area of the base and h the height from the base to the apex. This works for any location of the apex, provided that h is measured as the perpendicular distance from the plane which contains the base.

The formula can be formally proved using calculus: By similarity, the dimensions of a cross section parallel to the base increase linearly from the apex to the base. Then, the cross section at any height y is the base scaled by a factor of 1 - \tfrac{y}{h}, where h is the height from the base to the apex. 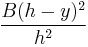Since the area of any shape is multiplied by the square of the shape's scaling factor, the area of a cross section at height y is \frac{B(h - y)^2}{h^2}. The volume is given by the integral

\frac{B}{h^2} \int_0^h (h-y)^2 \, dy = \frac{-B}{3h^2} (h-y)^3 \bigg|_0^h = \tfrac{1}{3}Bh.

The volume of a pyramid whose base is a regular n-sided polygon with side length s and whose height is h is therefore:

V = \frac{n}{12}hs^2 \cot\frac{\pi}{n}.

The volume of a pyramid whose base is a regular n-sided polygon with radius R is therefore:

V = \frac{nR^2h}{6} \sin{\frac{2\pi}{n}}.

This property can be used to derive the volume for cones, as well. See also cone.

Surface area

The surface area of a pyramid is 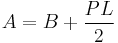A= B + \frac{PL}{2} where B is the base area, P is the base perimeter and L is the slant height.

See also

External links

Polyhedron navigator
Platonic solids (regular)
Archimedean solids
(Semiregular/Uniform)
truncated tetrahedron · cuboctahedron · truncated cube · truncated octahedron · rhombicuboctahedron · truncated cuboctahedron · snub cube · icosidodecahedron · truncated dodecahedron · truncated icosahedron · rhombicosidodecahedron · truncated icosidodecahedron · snub dodecahedron
Catalan solids
(Dual semiregular)
triakis tetrahedron · rhombic dodecahedron · triakis octahedron · tetrakis cube · deltoidal icositetrahedron · disdyakis dodecahedron · pentagonal icositetrahedron · rhombic triacontahedron · triakis icosahedron · pentakis dodecahedron · deltoidal hexecontahedron · disdyakis triacontahedron · pentagonal hexecontahedron
Dihedral regular
dihedron · hosohedron
Dihedral uniform
prisms · antiprisms
Duals of dihedral uniform
bipyramids · trapezohedra
Dihedral others
pyramids · truncated trapezohedra  · gyroelongated bipyramid  · cupola  · bicupola  · pyramidal frusta
Degenerate polyhedra are in italics.